Spatiotemporal Modeling & Learning for Dynamic Networks

Ph.D. Research: Integrating Stochastic Geometry, Queueing Theory, and Reinforcement Learning for Network Stability.

1. Research Background & Motivation

In large-scale wireless networks, performance is governed by the intricate coupling between spatial topology (the location of base stations) and temporal dynamics (packet arrival and queueing processes). Traditional models often assume “full-buffer” traffic, which provides a pessimistic lower bound but fails to capture the bursty nature of modern communication.

Our research, conducted during the Ph.D. at IETR & CNRS, focuses on characterizing the fundamental stability regions of random downlink cellular networks where the service rate of each node is coupled with the interference state of the entire network.

Dynamic Cellular Network Stability Analysis visa stochastic Geometry and Reinforcement Learning.

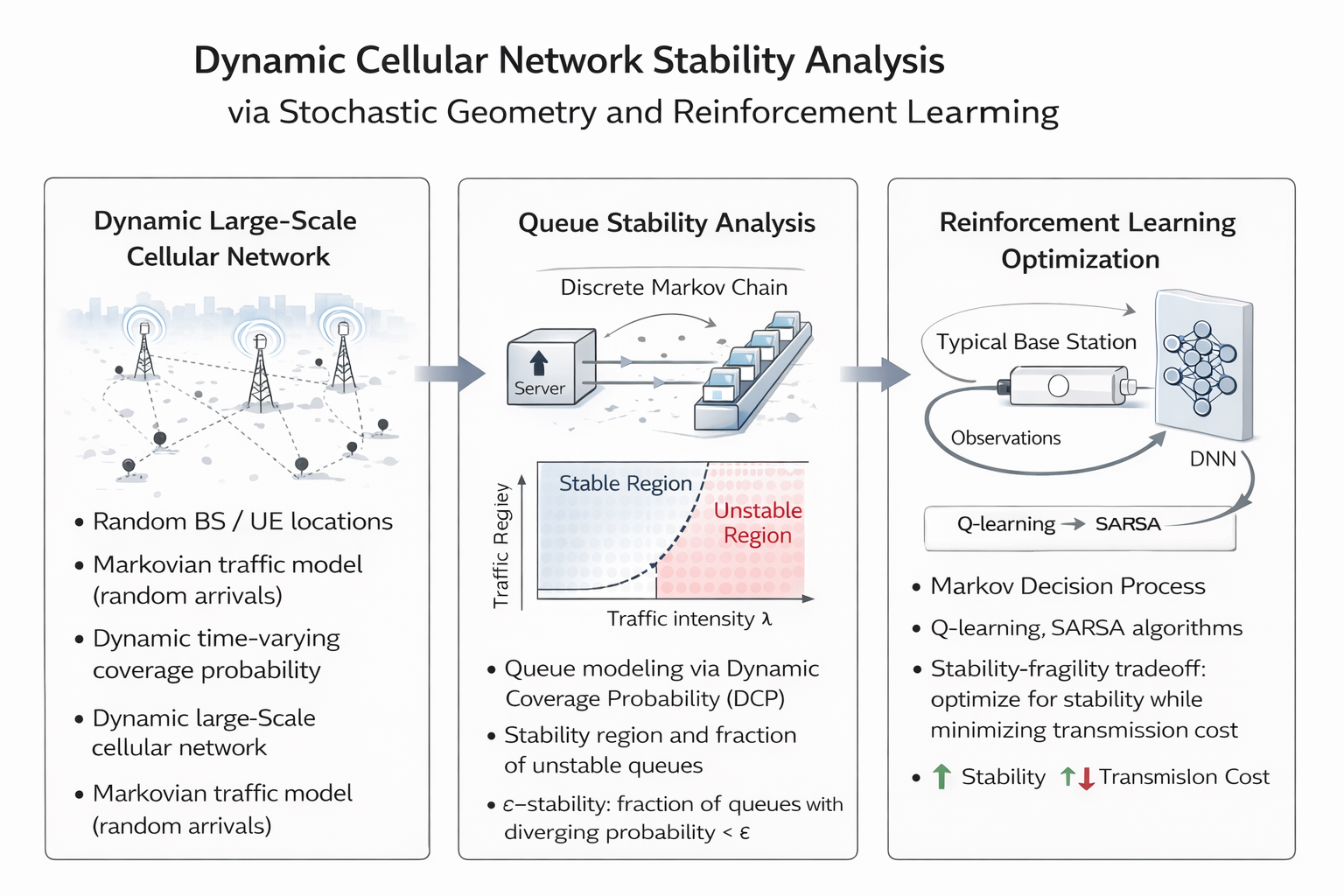
2. Methodology: From Stochastic Geometry to Queueing Theory

We propose a unified framework to analyze the interaction between the physical layer (SINR) and the data link layer (Queues).

Interacting Queueing Systems

Unlike independent queue models, we account for the spatiotemporal correlation of interference. The service rate of a typical user depends on the active state of interfering base stations, which in turn depends on their respective queue statuses.

  • Discrete-Time Markov Chains (DTMC): Used to model the evolution of buffers and capture the steady-state coverage probability.
  • Finite vs. Infinite Buffers: We derived analytical expressions for packet loss probability and mean waiting delay, bridging the gap between theoretical stability and practical buffer constraints.

The $\epsilon$-Stable Region

A key theoretical contribution is the definition of the $\epsilon$-stable region. While the classical stability region identifies when at least one queue diverges, the $\epsilon$-stable region quantifies the proportion of unstable nodes in a large-scale random network. This provides a fine-grained reliability metric for Communication Service Providers (CSPs).

3. Learning-based Resource Allocation

To address the complexity of joint spatial-dynamic optimization, we leveraged Reinforcement Learning (RL) to find optimal transmission policies.

MDP Framework & RL Algorithms

The network dynamics are formulated as a Markov Decision Process (MDP) where the typical base station acts as an agent.

  • Optimization Goal: Minimize the total cost, balancing transmission power (cost of action) and buffer latency (cost of waiting).
  • Robustness: Using Q-Learning and SARSA algorithms, we demonstrated that learning-based policies can maintain the same stability region as “greedy” policies while significantly reducing transmission costs by adapting to traffic fluctuations and local interference.

Technical Highlights

  • Mathematical Tools: Stochastic Geometry (Slivnyak’s & Campbell’s Theorems), Birth-Death Processes, Bellman Equations.
  • Key Metrics: Dynamic Coverage Probability, $\epsilon$-Stability, Packet Loss Rate, Mean Queue Delay.
  • Qiong Liu and Chung Shue Chen, “Queue-Aware RL Scheduling with Stability Bounds in Large-Scale Cellular Networks,” in Proc. IEEE Wireless Communications and Networking Conference (WCNC), 2026. (Accepted)
  • Qiong Liu, “Performance Analysis of Dynamic Downlink Cellular Networks,” Ph.D. Dissertation, Sorbonne University / IETR & CNRS, June 2022.
  • Qiong Liu, Jean-Yves Baudais, and Philippe Mary, “The $\epsilon$-stable region analysis in dynamic downlink cellular networks,” in 2022 IEEE 95th Vehicular Technology Conference (VTC2022-Spring), 2022.
  • Qiong Liu, Philippe Mary, and Jean-Yves Baudais, “Politiques de transmission basées sur l’apprentissage par renforcement dans les réseaux cellulaires dynamiques et aléatoires,” in Colloque GRETSI, 2022.
  • Qiong Liu, Jean-Yves Baudais, and Philippe Mary, “Queue analysis with finite buffer by stochastic geometry in downlink cellular networks,” in 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), 2021.
  • Qiong Liu, Jean-Yves Baudais, and Philippe Mary, “A tractable coverage analysis in dynamic downlink cellular networks,” in 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), 2020.